05316 BLUE MAD SEC – was Sie schon immer über EnPIs wissen wollten
|
Die in diesem Werk bisher vorgestellten Arbeitsmittel zur Bestimmung und Anwendung von EnPIs haben sich als sehr nützlich erwiesen. Dennoch tauchen immer wieder Fragen auf, die in diesem Beitrag beantwortet werden. Die benötigten Berechnungsvorlagen werden dazu in einer EnPI-Toolbox bereitgestellt. Arbeitshilfen: von: |
1 Einleitung
Trotz der Klarstellungen und Inhalte der ISO 50006, die es schon seit 2014 gibt und die 2023 neu erschienen ist (seit Februar 2025 auch auf deutsch), ist es erstaunlich, wie oft noch ungeeignete Energieleistungskennzahlen in Audits präsentiert werden. Spezifische EnPIs, sog. SEC, beherrschen das Feld, obwohl sie nur in wenigen Fällen die Realität abbilden können. Unterstützt wird dies durch Anforderungen in Reporting-Vorgaben nach ESRS oder durch den Konzern. SEC sind ein Spezialfall, der möglich ist, wenn es eine zu vernachlässigende Grundlast gibt, b0 also nahezu 0 ist (weitere Details dazu weiter unten).
Seit Inkrafttreten der ISO 50001:2018 konnten Leserinnen und Leser dieses Werks verschiedene Beiträge zu EnPIs lesen und haben Arbeitshilfen erhalten, um selbst normkonform EnPIs zu bestimmen und korrekt anzuwenden. Im Beitrag „ISO 50006 und mehr – praktische Lösungen für die Bewertung der energiebezogenen Leistung von SEUs und der gesamten Organisation” (s. Kap. 05315) wurde nicht nur die neue ISO 50006 im Detail vorgestellt, sondern auch eine detaillierte praktische Anleitung gegeben, wie geeignete EnPIs bestimmt und auf die gesamte Organisation angewendet werden können.
Dieser Beitrag möchte im FAQ-Stil weitere Hilfestellung und Klärung bieten. Um langes Suchen im Werk zu vermeiden, wurden die erforderlichen Arbeitsmittel in einer EnPI-Toolbox in Excel zusammengestellt.[
05316.xlsx]
05316.xlsx]Die Box enthält sechs Arbeitsblätter:
| • | Regression (1): Dieses Arbeitsblatt enthält das Ergebnis einer Regression in Excel, zusätzlich den Residuenplot gegen die Zeit und einen Q-Q-Plot mit den Residuen, beides kein Excel Standard. (s. auch Kap. 05315) |
| • | Monatsvergleich (2): Vorlage, um die aktuellen Monatsverbräuche mit den Baseline-Werten in der Regel des Vorjahres zu vergleichen; gegenüber der Ursprungsversion wurde die Visualisierung verbessert und die Dokumentation bei Abweichungen ergänzt. (s. auch Kap. 05315) |
| • | Jahresvergleich Forecast (3) und Jahresvergleich Backcast (4) in Version 3; dabei handelt es sich um die Leistungsbewertungstools, die seit ca. 2020 nach und nach weiterentwickelt wurden. Sie ermöglichen u. a. Fehlerbetrachtungen und können nicht routinemäßige Ereignisse (NRE) berücksichtigen. (s. auch Kap. 05314) |
| • | Gesamtleistung (5) mit Anleitung (6): Dabei handelt es sich um eine Vorlage in Anlehnung an Anhang G der ISO 50006:2023; um den Umgang zu erleichtern, wurden die Filterfunktion aktiviert und die Ebenen Energieträger und SEUs optisch unterschieden. (s. auch Kap. 05315) |
FAQs aus der Praxis
Mit diesem Rüstzeug und einer Statistiksoftware wie z. B. dem Regressionsmodul in Excel lassen sich geeignete EnPIs bestimmen und normkonform anwenden. Damit ist nicht gesagt, dass es immer einfach ist. Die Beratungsprojekte und Audits haben gezeigt, dass es oft kleine Herausforderungen gibt. Aber sie sind lösbar. Die folgenden FAQs haben sich in der Praxis ergeben und dienen dazu, die Arbeitshilfen richtig und geschickt anzuwenden.
Mit diesem Rüstzeug und einer Statistiksoftware wie z. B. dem Regressionsmodul in Excel lassen sich geeignete EnPIs bestimmen und normkonform anwenden. Damit ist nicht gesagt, dass es immer einfach ist. Die Beratungsprojekte und Audits haben gezeigt, dass es oft kleine Herausforderungen gibt. Aber sie sind lösbar. Die folgenden FAQs haben sich in der Praxis ergeben und dienen dazu, die Arbeitshilfen richtig und geschickt anzuwenden.
2.1 Warum sagt man, dass die Grundlast ungleich 0 bei der einfachen linearen Regression nicht vernachlässigt werden darf, obwohl sie genaugenommen manchmal unbekannt ist und sogar negativ sein kann?
Die schnelle Antwort:
Weil es sich bei der Konstante b0 (= y-Achsenabschnitt des Energieverbrauchs) oft gar nicht um die reale Grundlast handelt. Lediglich für die Fälle, wo die unabhängigen Variablen (x-Werte) wie z. B. Heizgradtage nahe an 0 herankommen, kann ein signifikanter, von 0 abweichender b0-Wert als Grundlast bezeichnet werden. In allen anderen Fällen handelt es sich bei b0 (ungleich 0) um eine Konstante, die mehr oder weniger bedeutungslos ist und dennoch nicht vernachlässigt werden darf.
Statistisch betrachtet sorgt der Achsenabschnitt b0 dafür, dass die Residuen im Mittel 0 ergeben. Wenn man b0 (deutlich ungleich 0) ignorieren würde, zwingt man die Regressionsgerade durch 0, was in vielen Fällen weit entfernt von den realen Daten liegt und somit eine starke Verzerrung bewirkt.
2.2 Warum sollte man bei 12 Datensätzen einen Q-Q-Plot machen?
Die schnelle Antwort:
Weil bei 12 Datensätzen nicht davon ausgegangen werden kann, dass die Verteilung der Residuen näherungsweise normalverteilt ist. Dies kann erst ab ca. 30 Datensätzen angenommen werden. Die Normalverteilung der Residuen ist jedoch eine Grundvoraussetzung für den t-Test und F-Test. Liegt diese Normalverteilung nicht annähernd vor, so sind die p-Werte anzuzweifeln.
Ein Q-Q-Plot (Quantil-Quantil-Plot) ist ein grafisches Werkzeug in der Statistik, das dazu verwendet wird, um zu untersuchen, ob eine Datenmenge einer bestimmten theoretischen Verteilung, meist der Normalverteilung, folgt. Es zeigt die Quantile der beobachteten Daten gegen die Quantile einer theoretischen Verteilung auf, wodurch Abweichungen oder Übereinstimmungen sichtbar werden. Wenn die Daten dieser Verteilung folgen, liegen die Punkte auf einer diagonalen Geraden. Abweichungen von dieser Geraden weisen auf Unterschiede zwischen den Daten und der Verteilung hin, z. B. auf schiefe (asymmetrische Verteilung) oder starke Ausreißer.
Excel testet standardmäßig die Y-Werte (hier Energiewerte) auf Normalverteilung. Die Quantile der Normalverteilung liegen somit schon vor. Um die Residuen auf Normalverteilung zu prüfen, werden sie einfach über die Energiewerte kopiert und sortiert (nur die Residuen, nicht die Quantile).
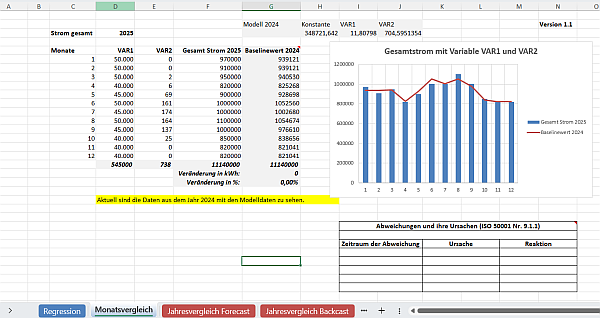
2.3 Warum sollte man beim Tool-Tabellenblatt „Monatsvergleich” die realen Daten des Modellzeitraums zusammen mit den modellierten Werten (=Baseline-Werten) auftragen?
Die schnelle Antwort:
Um zu sehen, ob kein Fehler vorliegt, denn wenn alles richtig ist, ist der reale Jahreswert 100 % identisch mit dem Baseline-Wert. Die EnPI ist BLUE, d. h. sie bildet den „Best Linear Unbiased Estimator”. Würde man bei der Modellierung Daten eliminieren, so weichen Realwert und Modellwert mehr oder weniger stark voneinander ab. Man spricht dann von einer Verzerrung (Bias).